Project Euler Problem 15 Solution

Project Euler Problem 15 Solution

Lattice paths

by {BetaProjects} | Project Euler & HackerRank

Project Euler Problem 15 Statement

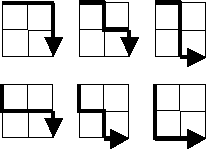
Starting at the top left corner of a 2×2 grid, there are 6 routes (without backtracking) to the bottom right corner.

4-by-4 grid

How many routes are there through a 20×20 grid?

Solution

funny, confusing, One-way signHere’s a similar question with more context.

"Starting at the top left corner of a grid, how many ways through town are possible using only south or east one–way streets and ending at the bottom right corner of the $n\times n$ grid?"

The valid paths for a $2\times 2$ grid shown in the example are the discreet (unique) permutations of {R, R, D, D}. We can list these as: {R, R, D, D}, {R, D, R, D}, {R, D, D, R}, {D, R, R, D}, {D, R, D, R} and {D, D, R, R}. You must have $2$ Rs (rights) and $2$ Ds (downs), the order not being important, and as long as you start from the top–left corner you will always end at the bottom–right corner.

A $4\times 4$ grid example

To find the number of paths in a $4\times 4$ grid, you’ll have to generate all the discreet permutations of {R, R, R, R, D, D, D, D}, where any combination of $4$ Rs and $4$ Ds will always be a valid path. If the Rs are first placed randomly in any $4$ of the $8$ open positions, then they are considered independent. The Ds are considered dependent because they have no choice but to be placed into the remaining slots.

For example, placing the $4$ Rs randomly in any of the available $8$ positions as {R, _, R, R, _, R, _, _} will dictate where the Ds get placed as {R, D, R, R, D, R, D, D}. You will have ${}^{8}C_{4} = 70$ valid combinations. This could be interpreted as: how many distinct ways can you shuffle the characters in the string “RRRRDDDD”.

Count the number of routes using the binomial coefficient

The number of contiguous routes for a square grid $(n\times n)$ is the central binomial coefficient or the center number in row $2n$ of Pascal’s triangle.  The rows start their numbering at $0$.

Pascal’s triangle

$${2n \choose n} = \frac{(2n)!}{n!~\times~n!}$$

The formula in general for any rectangular grid ($n~\times~m$) using the notation for the binomial coefficient is:

$${n+m \choose n} = \frac{(n~+~m)!}{n!~\times~m!}$$

HackerRank version

HackerRank logo

Solves all test cases for Hackerrank Project Euler Problem 15

HackerRank Project Euler 15: How many such routes are there through a $N\times M$ grid? As number of ways can be very large, print it modulo $(10^9+7)$. Runs up to $10^3$ test cases.

Python Source Code

import math
for _ in range(int(input())):
    N, M = map(int, input().split())
    print(math.comb(N+M, N)%1000000007)

Last Word

Another example assumes an $8\times 8$ grid:
“Place a single rook on the top left corner of an empty chess board. Count the number of tours to the bottom right corner, moving only right and down.”